昨天,一条大新闻炸翻了学术界:著名数学家、菲尔兹奖和阿贝尔奖双料得主阿提亚爵士(Sir Michael Francis Atiyah)宣布要在本月24号(也就是3天后)在海德堡宣讲自己对于黎曼猜想的证明。本文来自微信公众号:果壳(ID:Guokr42),作者: Yilong(群论研究公众号,清华大学丘成桐数学中心助理教授,UCLA数学PhD),原文标题:《黎曼猜想即将解开?这个“纯数学领域最重要的问题之一”,一篇文章讲清楚》。
数学家们有个笑话:怎样用世界上最难的方法挣到100万美元?
答:去证明黎曼猜想吧!
这是因为2000年5月的时候,美国克雷数学研究所(Clay Mathematics Institute, CMI)为了呼应1900年希尔伯特提出的23个历史性数学难题(也称“希尔伯特难题”)而设立的了一个成为“千禧难题”的数学问题挑战,一共7个问题,解出一道便可获得100万美元的奖金,挑战时间不限,题解必须发表在国际知名刊物上,并且要通过2年的验证期和专家小组的审核。
这7个问题中,以黎曼猜想最为著名,它是数论的分支解析数论的一大研究主题:质数的分布。据说,每年各大研究中心都会收到无数的神秘来信声称自己证明了“黎曼猜想”,数学家们跃跃欲试,科学界也一直热切关注。
所以备受瞩目的“黎曼猜想”究竟是个啥?跟我们有关系吗?
请收看《黎曼猜想,质数阴谋论,以及你不能说的秘密》:
一、为什么研究质数
黎曼猜想是一个数论里面的重要猜想,几百年来无人能解。那么,这么困难复杂的数学猜想,跟你有关系吗?请先看我瞎编的这样一个故事:
有一天,我的一个学数学的朋友给我发了一条微信,里面只有一串数,983040000。
我看到了之后,顿时觉得不妙,赶紧约这个朋友出来谈心。果然,他被女友甩了,悲伤绝望,有点想不开。
终于,在我的劝说下,朋友成功走出了阴霾,找回了面对人生的信心。
那么我是怎么知道这个朋友不开心的呢?因为983040000=219·31·54。这里面把质数从小到大排序:
• 第一小的质数(也就是2)出现了19次;
• 第二小的质数(也就是3)出现了1次;
• 第三小的质数(也就是5)出现了4次。
因此如果认为这代表一个单词,那么第一个位置上的字母是第19个字母(S),第二个位置上的字母是第1个字母(A),而第三个位置上的字母是第4个字母(D):合起来就是SAD。所以我知道这个朋友一定遇到伤心的事情了。
当然这个故事是我瞎编的。但是我们的生活中,无论是银行数据,还是国家机密,还是个人隐私,这些东西的保护都离不了密码,离不了加密的手段。
如果我想给你一串信息,又不想让其他人知道,怎么办呢?咱俩可以先商量好几个特别特别大的质数,比如说p、q和r。如果我想给你发送一个秘密的数字378,那么我实际上给你发送p3q7r8,一个巨大无比的数字。从我这里的角度,我可以很轻易的用计算机算出来这个乘法,得到结果发给你。从你的角度,你拿到了这个巨大的数字之后,只需要用p、q和r去除,就可以很快把幂解出来,得到378。
但是假设某个坏蛋截取了我发的这个秘密信息,那么想要知道内容,他就必须分解质因数。然而在不知道p、q和r的前提下,分解质因数是一个非常复杂和缓慢的过程,他可能需要好几百年才能破译出来。如此,我们的秘密就得到了保护。
这里面注意,p、q和r都必须要特别大,这时候分解质因数才会特别慢,甚至几百几千年。如果p、q和r分别是2,3和5,那么分解质因数就非常快了,可能一秒钟完事。
所以说,找到大的质数,了解质数都分布在哪里,是一个十分重要的事情。
二、质数规律
数学家多年研究,发现了一个惊人的事情:质数分布最大的规律,就是它几乎完全随机!
这里我们举一个简单的例子。假设我们从0到1之间均匀地随机挑一个实数。那么首先,我们知道这个实数的平均值应该是1/2。另一方面,这个随机的实数当然不一定是1/2,1/2只是在描述它平均的时候的样子。实际上它和1/2往往会有一定的正的或者负的偏差。
一个数学家发现的重大规律就是这个:平均来讲,1到n的正整数中一共有
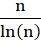 个质数。当然,这并不是说1到n里面一定有恰好n/ln(n)个质数。对于有的n来说,1到n里面的质数比较多一点。而对于有的n来说,1到n里面的质数比较少一点。但是随着n越来越大,n/ln(n)个质数的这个估计就必然会越来越准确。
个质数。当然,这并不是说1到n里面一定有恰好n/ln(n)个质数。对于有的n来说,1到n里面的质数比较多一点。而对于有的n来说,1到n里面的质数比较少一点。但是随着n越来越大,n/ln(n)个质数的这个估计就必然会越来越准确。
所以如果有人问你,1到10100里有多少个质数呀?你大可以拍拍脑袋说,我猜有
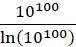 个质数,基本离正确答案不会差太远。一般来说,如果我们用π(n)来代表1到n里面的质数个数的话,那么
个质数,基本离正确答案不会差太远。一般来说,如果我们用π(n)来代表1到n里面的质数个数的话,那么
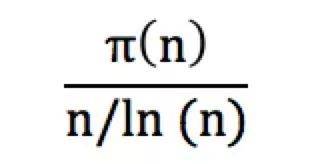
会如下图所示,逐渐趋于1。
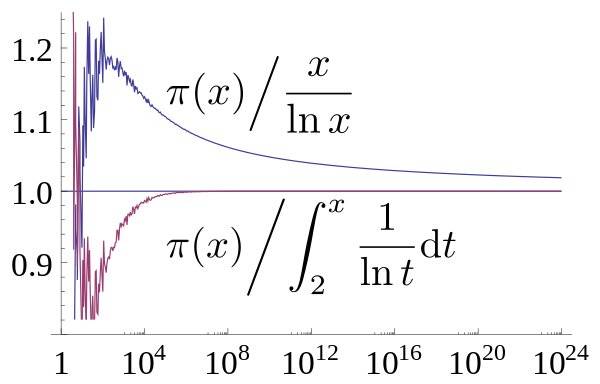
prime number theorem | wikipedia
事实上,随着人们对质数的了解越来越多,我们越来越发现,在宏观上来讲,质数几乎等于是按照这个n/ln(n)来进行的一种均匀分布。无论是你去数质数的个数,还是计算所有质数的和,还是研究孪生质数,都会发现质数呈现出一种惊人的宏观均匀性。这就好像有一个操场上有无数多个学生,尽管每个学生都在瞎走一气,毫无规律可循,但是总体来看,居然发现操场上每个平方米里都恰好塞了4个学生!这真是很难想象的事情。但是目前来说,几乎我们对质数的一切了解,都在指向这个方向。
这也进一步说明了,为什么质数特别适合做密码:因为质数本身就几乎是随机的,很难找到具体的规律,因此最适合作为加密的手段。
三、那么怎么研究质数
咱们先别想那么多。假设我们就想研究三个数字,1,2,3。
怎么研究呢?一种研究方法是,我们可以考虑研究这个函数:
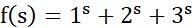
我宣称,这个函数的性质就包含了1,2,3的一切性质。为什么呢?
假设我们取s=10。那么这时候f(10)=1+1024+59049=60074。大家可以看到,这时候我们的f(10)和310没差多少。事实上,随着s越来越大,1s+2s相对于3s来说就越可以忽略不计。所以f(s)的这个s趋于无穷的极限的性质,其实就包含了一切的3的性质。
反过来,我们取s=-10。那么这时候f(10)=1+特别特别小+更加小,约等于1。可见,f(s)的这个s趋于负无穷的极限的性质,其实就包含了一切的1的性质。
那么怎么研究放在中间的2呢?这时候我们就要取复数了。考虑

当然,大家未必知道怎么计算复数幂,那么我直接把答案写出来吧。这时候,1s仍然是1,因为1的任何幂都是1。而2s是某个复数。最后,神奇的是,这个时候恰恰好3s=-1,哇!所以说
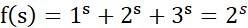
这个时候研究f(s)就等于是在研究2,因为1的部分和3的部分完全抵消掉了。
更广义的来说,如果我们想研究所有的正整数,那么只要我们搞清楚函数
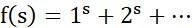 的一切性质,那么我们就搞清楚了全部的正整数。通过调整不同的s的值,我们就可以得到各种各样的抵消。
的一切性质,那么我们就搞清楚了全部的正整数。通过调整不同的s的值,我们就可以得到各种各样的抵消。
四、黎曼猜想
黎曼定义了一个ζ函数(念zeta):

这基本上和我们之前定义的差不多,只是差了一个负号。(黎曼定义这个负号,是因为希望s越大收敛性质越好。)这里面s可以去各种各样的复数,而对应的这个函数的值可能是无穷,可能是0,也可能是某个其他的复数。
黎曼猜想宣称,如果ζ(s)=0,那么s的实数部分一定是1/2。换句话说,s一定是1/2+b·i 的样子。
但是为什么我们要在乎ζ(s)=0的值呢?
一般来说,我们调整各种各样的s的值的时候,ζ(s)里面合数的部分往往随随便便就被质数的部分“吸收”了,而质数和质数的幂相对来说就很却难被消掉,往往会残留下来。那么如果你恰好发现,对于某个s,ζ(s)居然等于0,也就是说质数也都消光了。这就说明质数里面必然存在的某种针对这个s的结构。可以这样想,一般来说,我们每找到ζ(s)的一个根,就等于找到了一个质数里面的规律。
而一般来说,不妨这样认为:一个根s的实数部分是1/2时,这对应的往往是最“没用”的规律。一个根s的实数部分离1/2如果很遥远,就意味着质数存在某种惊人的巨大的结构性。(按照陶哲轩的话说,说明所有的质数们都一起针对这个s的值存在着某种惊天的阴谋!)所以黎曼猜想等于是在说,质数最大的规律,就是没有什么突出的规律。这样看来,黎曼猜想是一种悲观论调。
那么,如果黎曼猜想是正确的,那么说明质数是没有惊天的结构的,是几乎均匀的随机的。这等于说,我们进一步验证了“质数其实是按照n/ln(n)来进行随机均匀分布的”这个数学直觉。学过概率统计的同学可能知道,随机数往往符合大数定理。黎曼猜想正确的一个明显的后果就是,质数不仅仅似乎是按照n/ln(n)的概率均匀分布,而且还符合大数定理!而大数定理对于随机数的研究是至关重要的。同理,黎曼猜想对于质数的研究也是至关重要的。
因此,不出意外的,如果黎曼猜想是正确的,那么无数个我们对数论的猜想和直觉都会得到验证。
五、黎曼猜想错了,天会不会塌?
如果能够找到黎曼猜想的反例,那么反而是一个天大的喜事!为什么?因为一旦我们找到了一个ζ(s)=0的根,且s的实数部分远离了1/2,这就说明我们找到了一个关于质数的极其重要的规律!(发现了质数们的惊天阴谋!)这个规律很可能会我们对数的研究和认识带来惊天动地的飞跃。
恰恰是,如果黎曼猜想被证明了,反而无关紧要。大家早就猜测黎曼猜想是正确的了,很多数学家早就已经在假设黎曼猜想正确的前提下,继续往前研究了。所以如果有人证明黎曼猜想是正确的,这只不过是验证了我们一直以来都没错而已,却并不能够带来进步。
事实上,这有一个更有趣的现象。有很多的数学定理,比如说Littlewood定理,居然是这样证明的:
1) 假设黎曼猜想是正确的。那么质数具有非常美好的宏观均匀性。那么运用美好的宏观均匀性,证明了Littlewood定理。(Littlewood定理在这部分大概用了12页。)
2) 假设黎曼猜想是错误的。那么黎曼猜想的反例就会给出一种质数之间的惊人的结构。这种结构甚至可以让你一步登天,直接证明Littlewood定理。(Littlewood定理在这部分大概只用了半页。)
3) 所以说,无论黎曼定理是对的还是错的,反正Littlewood定理都是对的。证明完毕。
另外,大家可以看到,黎曼定理错误的时候,往往是证明更简洁更方便的时候!
总结一下,哪怕我们永远也不会知道黎曼猜想的对错,仅仅是黎曼猜想这个概念,就已经对数学产生了很大的推进作用。这就好像梦想一样,无论能否实现,都能让我们成为更好的人。
本文来自微信公众号:果壳(ID:Guokr42),作者: Yilong(群论研究公众号,清华大学丘成桐数学中心助理教授,UCLA数学PhD)。